Enzyme cost minimization
Main | Workflow | Model | Running ECM | Download
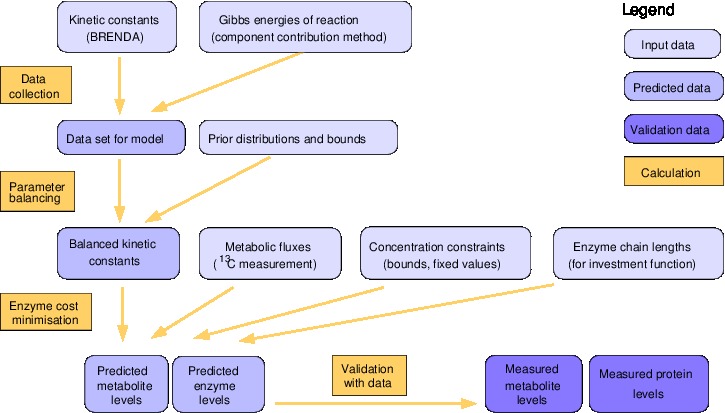
Workflow description
The aim of ECM is to predict optimal metabolite and enzyme levels for a given pathway model (including kinetic rate laws and kinetic parameters) and a predefined metabolic flux distribution to be realised. The algorithm for enzyme cost minimization consists of two main phases:
Kinetics phase
In the kinetics phase, we collect and adjust the model parameters and construct a model with energetically consistent fluxes (exclusion of infeasible cycles) and rate constants (satisfying Haldane relationships and Wegscheider conditions). To determine consistent model parameters, the collected rate constants and equilibrium constants are adjusted and completed by parameter balancing.
- Collect thermodynamic and kinetic data: standard chemical potentials mu , equilibrium constants Keq , Michaelis-Menten constants K M , forward and reverse catalytic constants kcat and kcat.
- Set some of these quantities to fixed values (if desired).
- Run parameter balancing (with priors, pseudo values, and upper and lower bounds) to obtain a complete, consistent set of rate constants.
Optimization phase
In the optimization phase, the desired pathway flux is realized by optimal enzyme and metabolite profiles.
- Set up the kinetic model (based on the given network, flux profile v, and model parameters). Redefine the reaction directions such that fluxes are positive, and update all parameters.
- Choose the bounds for metabolite concentrations (tight bounds or fixed values for metabolites with fixed concentrations, lower and upper bounds for the others).
- Determine a feasible metabolite profile s = ln c (a profile within the metabolite polytope) as a starting point for numerical optimization. We consider three alternatives: (i) Use linear programming to construct a set of extreme points in the polytope (with maximal and minimal metabolite levels s i ); the center of mass of these points is then taken as the starting point. (ii) Use the point in the polytope that is closest to the center of the predefined metabolite bounds (solution of a quadratic programming problem) as the starting point. (iii) Use the solution of the MDF problem (linear programming problem) as the starting point.
- Choose an EMC function and minimize it numerically with respect to s under the constraints defining the metabolite polytope.
- Compute the corresponding enzyme levels and cost.
- Based on the optimal enzyme cost, define a maximal tolerable cost (e.g., one percent higher than the optimal total cost) and compute individual tolerances for metabolite and enzyme levels as described in Methods.
- Validate the predicted enzyme and metabolite levels with experimental data.
In theory, a convex optimization should converge without problems. As a check, we can repeat the calculation with different starting points.